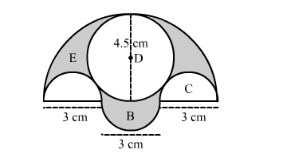
In the following figure, there are three semicircles,

(i) Area of the shaded region can be calculated as shown below,

Area of the shaded region = Area of the semi-circle with diameter of 9 cm − area of 2 semi-circles with radius 3cm − area of the circle with centre D + area of semi-circle with radius 3 cm

$\therefore$ Area of the shaded region $=\frac{\pi \times 4.5 \times 4.5}{2}-2 \times \frac{\pi \times 1.5 \times 1.5}{2}-\pi \times 2.25 \times 2.25+\frac{\pi \times 1.5 \times 1.5}{2}$

rea of the shaded region $=\frac{\pi \times 4.5 \times 4.5}{2}-\frac{\pi \times 1.5 \times 1.5}{2}-\pi \times 2.25 \times 2.25$

$\therefore$ Area of the shaded region $=\frac{\pi}{2}(20.25-2.25)-\pi \times 5.0625$

$\therefore$ Area of the shaded region $=\frac{\pi}{2}(18)-\pi \times 5.0625$

$\therefore$ Area of the shaded region $=9 \pi-\pi \times 5.0625$

$\therefore$ Area of the shaded region $=\pi(9-5.0625)$

$\therefore$ Area of the shaded region $=3.9375 \pi$

Substituting $\pi=\frac{22}{7}$ we get,

$\therefore$ Area of the shaded region $=3.9375 \times \frac{22}{7}$

$\therefore$ Area of the shaded region $=12.375$

Therefore, area of the shaded region is $12.375 \mathrm{~cm}^{2}$.

Now we will find the cost of painting the shaded region at the rate of 25 paise per cm2.

$\therefore \operatorname{Cos} t=12.375 \times 25$

$\therefore \operatorname{Cos} t=309.375$ paise

$\therefore \operatorname{Cost}=\operatorname{Rs} 3$

Therefore, cost of painting the shaded region to the nearest rupee is Rs 3 .