In the following figure, two circles with centres A and B touch each other at the point C.

Solution:

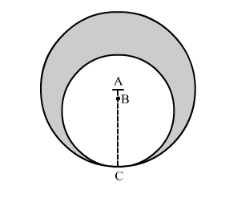
Area of the shaded region can be calculated as shown below,

Area of the shaded region = Area of circle with radius AC − area of circle with radius BC

We have given radius of the outer circle that is 8 cm but we don’t know the radius of the inner circle.

We can calculate the radius of the inner circle as shown below,

$B C=A C-A B$

$\therefore B C=8-3$

 

$\therefore B C=5$

$\therefore$ Area of the shaded region $=\pi \times 8 \times 8-\pi \times 5 \times 5$

$\therefore$ Area of the shaded region $=\pi \times 64-\pi \times 25$

 

$\therefore$ Area of the shaded region $=\pi \times 39$

Substituting $\pi=\frac{22}{7}$ we get,

$\therefore$ Area of the shaded region $=\frac{22}{7} \times 39$

$\therefore$ Area of the shaded region $=122.57$

Therefore, area of the shaded region is $122.57 \mathrm{~cm}^{2}$.