Question:
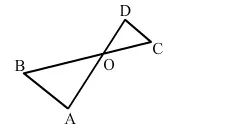
In the given figure $\triangle O A B \sim \triangle O C D$. If $A B=8 \mathrm{~cm}, B O=6.4 \mathrm{~cm}, O C=3.5$ and $C D=5 \mathrm{~cm}$, Find
(i) OA
(ii) DO.
Solution:
(i) Let OA be x cm.
$\because \triangle O A B \sim \triangle O C D$
$\therefore \frac{O A}{O C}=\frac{A B}{C D}$
$\Rightarrow \frac{x}{3.5}=\frac{8}{5}$
$\Rightarrow x=\frac{8 \times 3.5}{5}=5.6$
Hence, OA = 5.6 cm
(ii) Let OD be y cm
$\because \triangle O A B \sim \triangle O C D$
$\therefore \frac{A B}{C D}=\frac{O B}{O D}$
$\Rightarrow \frac{8}{5}=\frac{6.4}{y}$
$\Rightarrow y=\frac{6.4 \times 5}{8}=4$
Hence, DO = 4 cm
