Question:
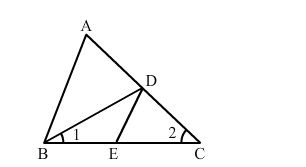
In the given figure, $\angle 1=\angle 2$ and $\frac{A C}{B D}=\frac{C B}{C E}$.
Prove that ∆ ACB ∼ ∆ DCE.
Solution:
We have:
$\frac{A C}{R D}=\frac{C B}{C F}$
$\Rightarrow \frac{A C}{C B}=\frac{B D}{C E}$
$\Rightarrow \frac{A C}{C B}=\frac{C D}{C E}($ Since, $B D=D C$ as $\angle 1=\angle 2)$
Also, $\angle 1=\angle 2$
i.e, $\angle D B C=\angle A C B$
Therefore, by SAS similarity theorem, we get:
$\triangle A C B \sim \triangle D C E$
