In the given figure, a ∆ABC has been given in which AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm.

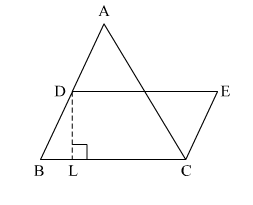
In ∆ABC,
The sides of the triangle are of length 7.5 cm, 6.5 cm and 7 cm.
∴ Semi-perimeter of the triangle is

$s=\frac{7.5+6.5+7}{2}=\frac{21}{2}=10.5 \mathrm{~cm}$

∴ By Heron's formula,

Area of $\Delta A B C=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{10.5(10.5-7.5)(10.5-6.5)(10.5-7)}$

$=\sqrt{10.5(3)(4)(3.5)}$

$=21 \mathrm{~cm}^{2} \quad \ldots(2)$

Now,
Area of parallelogram DBCE = Area of ∆ABC

$=21 \mathrm{~cm}^{2}$

Also,
Area of parallelogram DBCE = base × height

$\Rightarrow 21=B C \times D L$

$\Rightarrow 21=7 \times D L$

$\Rightarrow D L=\frac{21}{7}=3 \mathrm{~cm}$

Hence, the height DL of the parallelogram is 3 cm.