In the given figure, a circle touches all the four sides of a quadrilateral

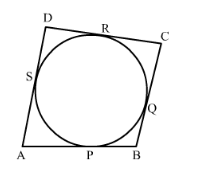
The figure given in the question is below.

From the property of tangents we know that, the length of two tangents drawn from the same external point will be equal. Therefore we have the following,

SA = AP

For our convenience, let us represent SA and AP by a

PB = BQ

Let us represent PB and BQ by b

QC = CR

Let us represent QC and CR by c

DR = DS

Let us represent DR and DS by d

It is given in the problem that,

AB = 6

By looking at the figure we can rewrite the above equation as follows,

AP + PB = 6

a + b = 6

b = 6 − a …… (1)

Similarly we have,

BC = 7

BQ + QC = 7

b + c = 7

Let us substitute the value of b which we have found in equation (1). We have,

6 − a + c = 7

c = a + 1 …… (2)

CD = 4

CR + RD = 4

c + d = 4

Let us substitute the value of c which we have found in equation (2).

a + 1 + d = 4

a + d =3

As per our representations in the previous section, we can write the above equation as follows,

SA + DS = 3

By looking at the figure we have,

AD = 3

Thus we have found that length of side AD is 3 cm.