In the given figure, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF is
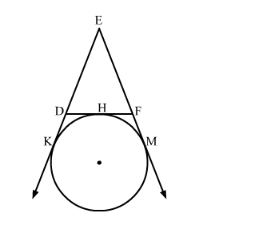
(a) 18 cm (b) 13.5 cm (c) 12 cm (d) 9 cm [CBSE 2012]
In the given figure, DH and DK are tangents drawn to the circle from an external point D.
∴ DH = DK (Lengths of tangents drawn from an external point to a circle are equal)
FH and FM are tangents drawn to the circle from an external point F.
∴ FH = FM (Lengths of tangents drawn from an external point to a circle are equal)
EK and EM are tangents drawn to the circle from an external point E.
∴ EM = EK = 9 cm (Lengths of tangents drawn from an external point to a circle are equal)
Now,
Perimeter of ΔEDF = ED + DF + EF
= ED + (DH + FH) + EF
= ED + (DK + FM) + EF (DH = DK and FH = FM)
= (ED + DK) + (FM + EF)
= EK + EM
= 9 cm + 9 cm
= 18 cm
Thus, the perimeter of ΔEDF is 18 cm.
Hence, the corrrect answer is option A.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.