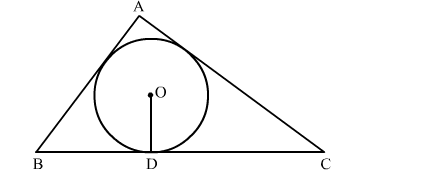
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm

Construction: Join OA, OB, OC, OE ⊥ AB at E and OF ⊥ AC at F

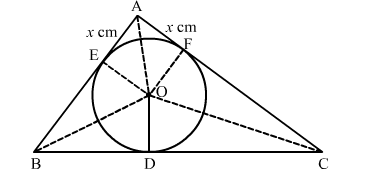
We know that tangent segments to a circle from the same external point are congruent.
Now, we have
AE = AF, BD = BE = 4 cm and CD = CF = 3 cm
Now,

Area $(\triangle \mathrm{ABC})=$ Area $(\triangle \mathrm{BOC})+$ Area $(\triangle \mathrm{AOB})+$ Area $(\triangle \mathrm{AOC})$

$\Rightarrow 21=\frac{1}{2} \times \mathrm{BC} \times \mathrm{OD}+\frac{1}{2} \times \mathrm{AB} \times \mathrm{OE}+\frac{1}{2} \times \mathrm{AC} \times \mathrm{OF}$

$\Rightarrow 42=7 \times 2+(4+x) \times 2+(3+x) \times 2$

$\Rightarrow 21=7+4+x+3+x$

$\Rightarrow 21=14+2 x$

$\Rightarrow 2 x=7$

$\Rightarrow x=3.5 \mathrm{~cm}$

 ∴ AB = 4 + 3.5 = 7.5 cm and AC = 3 + 3.5 = 6.5 cm