In the given figure, AB || CD and a transversal t cuts them at E and F respectively.

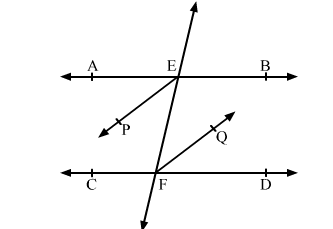
It is given that, AB || CD and t is a transversal.

∴ ∠AEF = ∠EFD           .....(1)         (Pair of alternate interior angles)

EP is the bisectors of ∠AEF.        (Given)

$\therefore \angle \mathrm{AEP}=\angle \mathrm{FEP}=\frac{1}{2} \angle \mathrm{AEF}$

⇒ ∠AEF = 2∠FEP          .....(2)

Also, FQ is the bisectors of ∠EFD.

$\therefore \angle \mathrm{EFQ}=\angle \mathrm{QFD}=\frac{1}{2} \angle \mathrm{EFD}$

⇒ ∠EFD = 2∠EFQ         .....(3)

From (1), (2) and (3), we have

2∠FEP = 2∠EFQ

⇒ ∠FEP = ∠EFQ

Thus, the lines EP and FQ are intersected by a transversal EF such that the pair of alternate interior angles formed are equal. 

∴ EP || FQ        (If a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel)