Question:
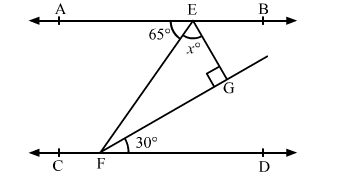
In the given figure, AB || CD and EF is a transversal. If ∠AEF = 65°, ∠DFG = 30°, ∠EGF = 90° and ∠GEF = x°, find the value of x.
Solution:
It is given that, AB || CD and EF is a transversal.
∴ ∠EFD = ∠AEF (Pair of alternate angles)
⇒ ∠EFD = 65°
⇒ ∠EFG + ∠GFD = 65°
⇒ ∠EFG + 30° = 65°
⇒ ∠EFG = 65° − 30° = 35°
In ∆EFG,
∠EFG + ∠GEF + ∠EGF = 180° (Angle sum property)
⇒ 35° + x + 90° = 180°
⇒ 125° + x = 180°
⇒ x = 180° − 125° = 55°
Thus, the value of x is 55°.
