In the given figure, AB || DE and BD || FG such that ∠ABC = 50° and ∠FGH = 120°. Find the values of x and y.
Question:
In the given figure, AB || DE and BD || FG such that ∠ABC = 50° and ∠FGH = 120°. Find the values of x and y.
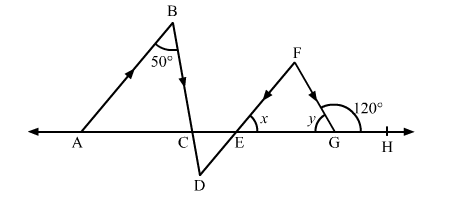
Solution:
We have, ∠FGE + ∠FGH = 180° (Linear pair of angles)
∴ y + 120° = 180°
⇒ y = 180° − 120° = 60°
Now, AB || DF and BD is the transversal.
∴ ∠ABD = ∠BDF (Pair of alternate angles)
⇒ ∠BDF = 50°
Also, BD || FG and DF is the transversal.
∴ ∠BDF = ∠DFG (Pair of alternate angles)
⇒ ∠DFG = 50° .....(1)
In ∆EFG,
∠FGH = ∠EFG + ∠FEG (Exterior angle of a triangle is equal to the sum of the two opposite interior angles)
⇒ 120° = 50° + x [Using (1)]
⇒ x = 120° − 50° = 70°
Thus, the values of x and y are 70° and 60°, respectively.
