In the given figure, AB is a chord of a circle with centre O and AB is produced to C such that BC = OB.
Question:
In the given figure, AB is a chord of a circle with centre O and AB is produced to C such that BC = OB. Also, CO is joined and produced to meet the circle in D. If ∠ACD = y° and ∠AOD = x°, prove that x = 3y.
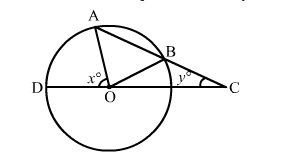
Solution:
We have:
OB = OC, ∠BOC = ∠BCO = y
External ∠OBA = ∠BOC + ∠BCO = (2y)
Again, OA = OB, ∠OAB = ∠OBA = (2y)
External ∠AOD = ∠OAC + ∠ACO
Or x = ∠OAB + ∠BCO
Or x = (2y) + y = 3y
Hence, x = 3y
