In the given figure, AB || PQ. Find the values of x and y.

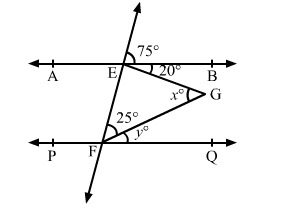
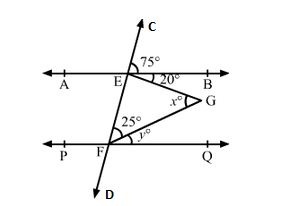
Given, $A B \| P Q$.

Let CD be the transversal cutting AB and PQ at E and F, respectively.
Then,

$\angle C E B+\angle B E G+\angle G E F=180^{\circ} \quad$ [Since CD is a straight line]

$\Rightarrow 75^{\circ}+20^{\circ}+\angle G E F=180^{\circ}$

$\Rightarrow \angle G E F=85^{\circ}$

We know that the sum of angles of a triangle is 180°">180°180°.

$\therefore \angle G E F+\angle E G F+\angle E F G=180$

$\Rightarrow 85^{\circ}+x+25^{\circ}=180^{\circ}$

$\Rightarrow 110^{\circ}+x=180^{\circ}$

$\Rightarrow x=70^{\circ}$

And

$\angle F E G+\angle B E G=\angle D F Q \quad[$ Corresponding Angles $]$

$\Rightarrow 85^{\circ}+20^{\circ}=\angle D F Q$

$\Rightarrow \angle D F Q=105^{\circ}$

$\angle E F G+\angle G F Q+\angle D F Q=180^{\circ} \quad[$ Since CD is a straight line $]$

$\Rightarrow 25^{\circ}+y+105^{\circ}=180^{\circ}$

$\Rightarrow y=50^{\circ}$

$\therefore x=70^{\circ}$ and $y=50^{\circ}$