Question:
In the given figure, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.
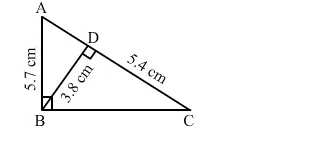
Solution:
It is given that ABC is a right angled triangle and BD is the altitude drawn from the right angle to the hypotenuse.
In $\triangle B D C$ and $\triangle A B C$, we have :
$\angle A B C=\angle B D C=90^{\circ}$ (given)
$\angle C=\angle C$ (common)
By AA similarity theorem, we get:
$\triangle B D C \sim \triangle A B C$
$\frac{A B}{B D}=\frac{B C}{D C}$
$\Rightarrow \frac{5.7}{3.8}=\frac{B C}{5.4}$
$\Rightarrow B C=\frac{5.7}{3.8} \times 5.4$
$=8.1$
Hence, BC = 8.1 cm
