In the given figure, $\triangle A B C$ and $\triangle D B C$ have the same base $B C$. If $A D$ and $B C$ intersect at $O$, prove that $\frac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta D B C)}=\frac{A O}{D O}$.
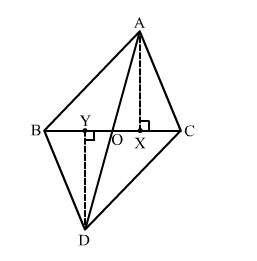
Construction : Draw $\mathrm{AX} \perp \mathrm{CO}$ and DY $\perp \mathrm{BO}$.
As,
$\frac{\operatorname{ar}(\triangle \mathrm{ABC})}{\operatorname{ar}(\triangle \mathrm{DBC})}=\frac{1 / 2 \times \mathrm{AX} \times \mathrm{BC}}{1 / 2 \times \mathrm{DY} \times \mathrm{BC}}$
$\Rightarrow \frac{\operatorname{ar}(\triangle \mathrm{ABC})}{\operatorname{ar}(\triangle \mathrm{DBC})}=\frac{\mathrm{AX}}{\mathrm{DY}} \quad \cdots(\mathrm{i})$
In $\triangle \mathrm{ABC}$ and $\triangle \mathrm{DBC}, \angle \mathrm{AXY}=\angle \mathrm{DYO}=90^{\circ}($ By construction $) \angle \mathrm{AOX}=\angle \mathrm{DOY}($ Vertically opposite angles $) \therefore \triangle \mathrm{AXO} \sim \triangle \mathrm{DYO}$
$($ By AA criterion $) \therefore \frac{\mathrm{AX}}{\mathrm{DY}}=\frac{\mathrm{AO}}{\mathrm{DO}} \quad($ Thales's theorem $) \ldots(\mathrm{ii})$ From $(\mathrm{i})$ and $(\mathrm{ii})$, we have : $\frac{\mathrm{ar}(\triangle \mathrm{ABC})}{\mathrm{ar}(\triangle \mathrm{DBC})}=\frac{\mathrm{AX}}{\mathrm{DY}}=\frac{\mathrm{AO}}{\mathrm{DO}}$ or, $\frac{\mathrm{ar}(\triangle \mathrm{ABC})}{\mathrm{ar}(\triangle \mathrm{DBC})}=$
$\frac{\mathrm{AO}}{\mathrm{DO}}$
This completes the proof.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.