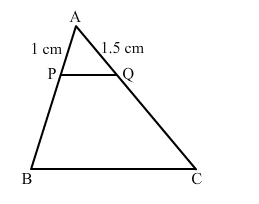
In the given figure, ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm,
In the given figure, $A B C$ is a triangle and $P Q$ is a straight line meeting $A B$ in $P$ and $A C$ in $Q$. If $A P=1 \mathrm{~cm}, P B=3 \mathrm{~cm}, A Q=1.5 \mathrm{~cm}, Q C=4.5 \mathrm{~cm}$, prove that are of $\triangle A P Q$ is $\frac{1}{16}$ of the area of $\triangle A B C$.
We have:
$\frac{A P}{A B}=\frac{1}{1+3}=\frac{1}{4}$ and $\frac{A Q}{A C}=\frac{1.5}{1.5+4.5}=\frac{1.5}{6}=\frac{1}{4}$
$\Rightarrow \frac{A P}{A B}=\frac{A Q}{A C}$
Also, $\angle A=\angle A$
By SAS similarity, we can conclude that $\triangle \mathrm{APQ} \sim \triangle \mathrm{ABC}$.
$\frac{\operatorname{ar}(\Delta A P Q)}{\operatorname{ar}(\Delta A B C)}=\frac{A P^{2}}{A B^{2}}=\frac{1^{2}}{4^{2}}=\frac{1}{16}$
$\Rightarrow \frac{\operatorname{ar}(\Delta A P Q)}{\operatorname{ar}(\Delta A B C)}=\frac{1}{16}$
$\Rightarrow \operatorname{ar}(\Delta A P Q)=\frac{1}{16} \times \operatorname{ar}(\Delta A B C)$
Hence proved.
