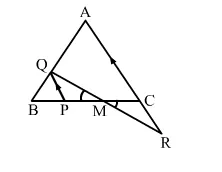
In the given figure, ABC is an equilateral triangle; PQ || AC and AC is produced to R such that CR = BP.

Since $\Delta \mathrm{ABC}$ is an equilateral $\Delta$, then

$\angle \mathrm{ABC}=\angle \mathrm{BCA}=\angle \mathrm{CAB}=60^{\circ}$

Since PQ $\| \mathrm{CA}$ and PC is a transversal, then

$\angle \mathrm{BPQ}=\angle \mathrm{BCA}=60^{\circ} \quad$ (Corresponding angles)

Since PQ $\| \mathrm{CA}$ and QA is a transversal, then

$\angle \mathrm{BQP}=\angle \mathrm{BAC}=60^{\circ} \quad$ (Corresponding angles)

Further, $\angle \mathrm{B}=60^{\circ}$

In $\Delta \mathrm{BPQ}$

$\angle \mathrm{B}=\angle \mathrm{BPQ}=\angle \mathrm{BQP}=60^{\circ}$

$\therefore \triangle \mathrm{BPQ}$ is an equilateral triangle.

i. e., $B P=P Q=B Q$

Now, $B P=C R$

$\Rightarrow \mathrm{PQ}=\mathrm{CR} \quad \ldots(1)$

Considering $\triangle \mathrm{MPQ}$ and $\triangle \mathrm{MCR}$, we get:

$\angle \mathrm{PQM}=\angle \mathrm{MRC} \quad$ (Alternate interior angles)

$\angle \mathrm{PMQ}=\angle \mathrm{CMR} \quad($ Vertically opposite angles $)$

$\mathrm{PQ}=\mathrm{CR} \quad$ [using (1)]

$\Delta \mathrm{MPQ} \cong \Delta \mathrm{MCR}$ (AAS criterion)

$\Rightarrow \mathrm{MP}=\mathrm{MC} \quad$ [Corresponding parts of congruent triangles are equal]

$\Rightarrow$ QR bisects PC.