In the given figure, Δ ABC is circumscribing a circle. Find the length of BC.

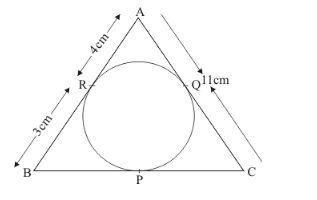
We are given the following figure

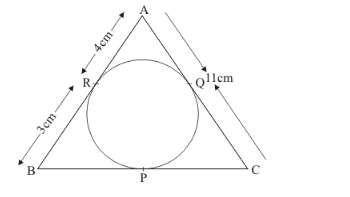
From the figure we get,

BC = BP + PC …… (1)

Now, let us find BP and PC separately.

From the property of tangents we know that when two tangents are drawn to a circle from a common external point, the length of the two tangents from the external point to the respective points of contact will be equal. Therefore we have,

BR = BP

It is given in the problem that BR = 3 cm. Therefore,

BP = 3 cm

Now let us find out PC.

Again using the same property of tangents which says that the length of two tangents drawn to a circle from the same external point will be equal, we have,

PC = QC…… (2)

From the figure we can see that,

QC = AC − AQ…… (3)

Again using the property that length of two tangents drawn to a circle from the same external point will be equal, we have,

AQ = AR

In the problem it is given that,

AR = 4 cm

Therefore,

AQ = 4 cm

Also, the length of AC is also given in the problem.

AC = 11 cm

Let us now substitute the values of AC and AQ in equation (3)

QC = 11 − 4

QC = 7

From equation (2) we can say that,

PC = 7

Finally, let us substitute the values of PC and BP in equation (1)

BC = BP + PC

BC = 3 + 7

BC = 10

Therefore, length of BC is 10 cm.