In the given figure, ABCD is a cyclic quadrilateral in which DC is produced to E and CF is drawn parallel to AB such that ∠ADC = 95° and ∠ECF = 20°.
Question:
In the given figure, ABCD is a cyclic quadrilateral in which DC is produced to E and CF is drawn parallel to AB such that ∠ADC = 95° and ∠ECF = 20°. Then, ∠BAD = ?
(a) 95°
(b) 85°
(c) 105°
(d) 75°
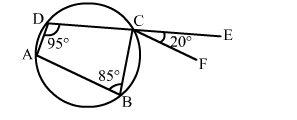
Solution:
(c) 105°
We have:
∠ABC + ∠ADC = 180°
⇒ ∠ABC + 95° = 180°
⇒∠ABC = (180° - 95°) = 85°
Now, CF || AB and CB is the transversal.
∴ ∠BCF = ∠ABC = 85° (Alternate interior angles)
⇒ ∠BCE = (85° + 20°) = 105°
⇒ ∠DCB = (180° - 105°) = 75°
Now, ∠BAD + ∠BCD = 180°
⇒ ∠BAD + 75° = 180°
⇒ ∠BAD = (180° - 75°) = 105°
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
