Question:
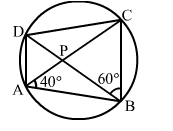
In the given figure, ABCD is a cyclic quadrilateral whose diagonals intersect at P such that ∠DBC = 60° and ∠BAC = 40°. Find
(i) ∠BCD,
(ii) ∠CAD.
Solution:
(i) ∠BDC = ∠BAC = 40° (Angles in the same segment)
In ΔBCD, we have:
∠BCD + ∠DBC + ∠BDC = 180° (Angle sum property of a triangle)
⇒ ∠BCD + 60° + 40° = 180°
⇒ ∠BCD = (180° - 100°) = 80°
(ii) ∠CAD = ∠CBD (Angles in the same segment)
= 60°
