In the given figure, ABCD is a quadrilateral in which AB = AD and BC = DC. Prove that
(i) AC bisects ∠A and ∠C,
(ii) BE = DE,
(iii) ∠ABC = ∠ADC.
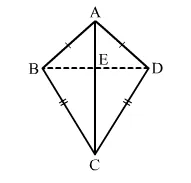
Given: ABCD is a quadrilateral in which AB = AD and BC = DC
(i)
In ∆ABC and ∆ADC, we have:
AB = AD (Given)
AC is common.
i.e., ∆ABC ≅ ∆ADC (SSS congruence rule)
∴ ∠BAC = ∠DAC and ∠BCA = ∠DCA (By CPCT)
Thus, AC bisects ∠A and ∠ C.
(ii)
Now, in ∆ABE and ∆ADE, we have:
AB = AD (Given)
∠BAE = ∠DAE (Proven above)
AE is common.
∴ ∆ABE ≅ ∆ADE (SAS congruence rule)
⇒ BE = DE (By CPCT)
(iii) ∆ABC ≅ ∆ADC (Proven above)
∴ ∠ABC = ∠ADC (By CPCT)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.