Question:
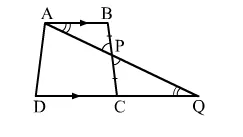
In the given figure, ABCD is a quadrilateral in which AB || DC and P is the midpoint of BC. On producing, AP and DC meet at Q. Prove that (i) AB = CQ, (ii) DQ = DC + AB.
Solution:
In $\triangle \mathrm{ABP}$ and $\triangle \mathrm{QCP}$, we have:
$\angle \mathrm{BPA}=\angle \mathrm{CPQ} \quad($ Vertically opposite angle $)$
$\angle \mathrm{PAB}=\angle \mathrm{PQC} \quad$ (Alternate angles)
$\mathrm{PB}=\mathrm{PC} \quad(\mathrm{P}$ is the midpoint)
$\triangle \mathrm{ABP} \cong \triangle \mathrm{QCP} \quad$ (AAS criterion)
$\therefore \mathrm{AB}=\mathrm{CQ} \quad$ (CPCT)
$\mathrm{DQ}=\mathrm{DC}+\mathrm{CQ}$
$\Rightarrow \mathrm{DQ}=\mathrm{DC}+\mathrm{AB} \quad$ (Proved, $\mathrm{AB}=\mathrm{CQ}$ )
Hence, proved.
