Question:
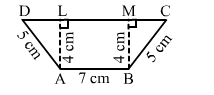
In the given figure ABCD is a trapezium such that AL ⊥ DC and BM ⊥ DC. If AB = 7 cm, BC = AD = 5 cm and AL = BM = 4 cm, then ar(trap. ABCD) = ?
(a) $24 \mathrm{~cm}^{2}$
(b) $40 \mathrm{~cm}^{2}$
(c) $55 \mathrm{~cm}^{2}$
(d) $27.5 \mathrm{~cm}^{2}$
Solution:
(b) $40 \mathrm{~cm}^{2}$
In right angled triangle MBC, we have:
$M C=\sqrt{5^{2}-4^{2}}=\sqrt{9}=3 \mathrm{~cm}$
In right angled triangle ADL, we have:
$D L=\sqrt{5^{2}-4^{2}}=\sqrt{9}=3 \mathrm{~cm}$
Now, CD = ML + MC + LD = 7 + 3 + 3 = 13 cm
$\therefore$ Area of the trapezium $=\frac{1}{2} \times$ (sum of parallel sides) $\times$ distance between them
$=\frac{1}{2} \times(13+7) \times 4$
$=40 \mathrm{~cm}^{2}$
