In the given figure, AD divides ∠BAC in the ratio 1 : 3 and AD = DB.

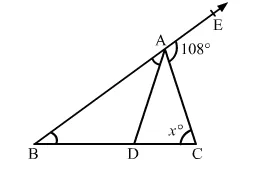
$\angle B A C+\angle C A E=180^{\circ} \quad[\because B E$ is a straight line $]$

$\Rightarrow \angle B A C+108^{\circ}=180^{\circ}$

$\Rightarrow \angle B A C=72^{\circ}$

Now, divide $72^{\circ}$ in the ratio $1: 3$.

$\therefore a+3 a=72^{\circ}$

$\Rightarrow a=18^{\circ}$

$\therefore a=18^{\circ}$ and $3 a=54^{\circ}$

Hence, the angles are $18^{\circ}$ and $54^{\circ}$

$\therefore \angle B A D=18^{\circ}$ and $\angle D A C=54^{\circ}$

Given,

$A D=D B$

$\Rightarrow \angle D A B=\angle D B A=18^{\circ}$

In $\Delta A B C$, we have:

$\angle B A C+\angle A B C+\angle A C B=180^{\circ} \quad$ [Sum of the angles of a triangle]

$\Rightarrow 72^{\circ}+18^{\circ}+x^{\circ}=180^{\circ}$

$\Rightarrow x^{\circ}=90^{\circ}$

$\therefore x=90$