Question:
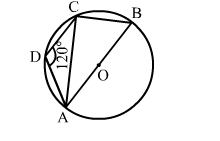
In the given figure, AOB is a diameter and ABCD is a cyclic quadrilateral. If ∠ADC = 120°, then ∠BAC = ?
(a) 60°
(b) 30°
(c) 20°
(d) 45°
Solution:
(b) 30°
We have:
∠ABC + ∠ADC = 180° (Opposite angles of a cyclic quadrilateral)
⇒ ∠ABC + 120° = 180°
⇒ ∠ABC = (180° - 120°) = 60°
Also, ∠ACB = 90° (Angle in a semicircle)
In ΔABC, we have:
∠BAC + ∠ACB + ∠ABC = 180° (Angle sum property of a triangle)
⇒ ∠BAC + 90° + 60° = 180°
⇒ ∠BAC = (180° - 150°) = 30°
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
