Question:
In the given figure, BA || ED and BC || EF. Show that ∠ABC + ∠DEF = 180°.
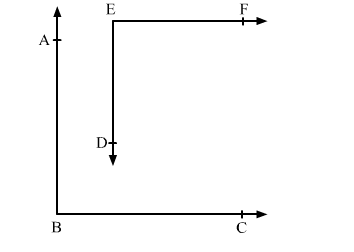
Solution:
It is given that, BA || ED and BC || EF.
Construction: Extend ED such that it intersects BC at G.
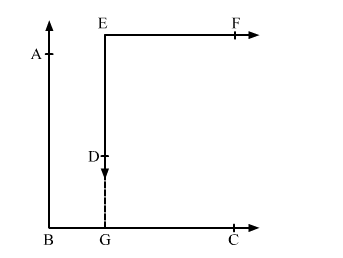
Now, BA || GE and BC is a transversal.
∴ ∠ABC = ∠EGC .....(1) (Pair of corresponding angles)
Also, BC || EF and EG is a transversal.
∴ ∠EGC + ∠GEF = 180° .....(2) (Interior angles on the same side of the transversal are supplementary)
From (1) and (2), we have
∠ABC + ∠GEF = 180°
Or ∠ABC + ∠DEF = 180°
