Question:
In the given figure, ∠CAB = 90° and AD ⊥ BC. Show that ∆ BDA ∼ ∆ BAC. If AC = 75 cm, AB = 1 m and BC = 1.25 m, find AD.
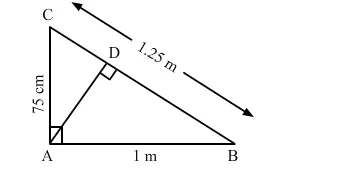
Solution:
In $\triangle B D A$ and $\triangle B A C$, we have :
$\angle B D A=\angle B A C=90^{\circ}$
$\angle D B A=\angle C B A \quad($ Common $)$
Therefore, by AA similarity theorem, $\triangle B D A \sim \triangle B A C$
$\Rightarrow \frac{A D}{A C}=\frac{A B}{B C}$
$\Rightarrow \frac{A D}{0.75}=\frac{1}{1.25}$
$\Rightarrow A D=\frac{0.75}{1.25}$
$=0.6 \mathrm{~m}$ or $60 \mathrm{~cm}$
