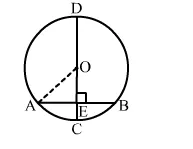
In the given figure, CD is the diameter of a circle with centre O and CD is perpendicular to chord AB.

(c) 7.5 cm
Let OA = OC = r cm.

Then $\mathrm{OE}=(r-3) \mathrm{cm}$ and $\mathrm{AE}=\frac{1}{2} \mathrm{AB}=6 \mathrm{~cm}$

Now, in right ΔOAE, we have:

$\mathrm{OA}^{2}=\mathrm{OE}^{2}+\mathrm{AE}^{2}$

$\Rightarrow(r)^{2}=(r-3)^{2}+6^{2}$

$\Rightarrow r^{2}=r^{2}+9-6 r+36$

⇒ 6r = 45

$\Rightarrow r=\frac{45}{6}=7.5 \mathrm{~cm}$

Hence, the required radius of the circle is 7.5 cm.