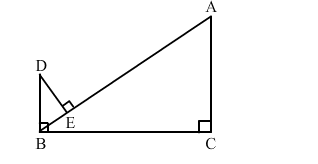
In the given figure, DB ⊥ BC, DE ⊥ AB and AC ⊥ BC.

In $\triangle B E D$ and $\triangle A C B$, we have:

$\angle B E D=\angle A C B=90^{\circ}$

$\because \angle B+\angle C=180^{\circ}$

$\therefore B D \| A C$

$\angle E B D=\angle C A B$ (Alternate angles)

Therefore, by AA similarity theorem, we get:

$\triangle B E D \sim \triangle A C B$

$\Rightarrow \frac{B E}{A C}=\frac{D E}{B C}$

$\Rightarrow \frac{B E}{D E}=\frac{A C}{B C}$

This completes the proof.