In the given figure, DE ∥ BC and DE : BC = 3 : 5.

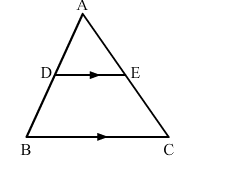
It is given that DE ∥">∥ BC.

$\therefore \angle A D E=\angle A B C$ (Corresponding angles)

$\angle A E D=\angle A C B$ (Corresponding angles)

Applying AA similarity theorem, we can conclude that $\triangle A D E \sim \triangle A B C$.

$\therefore \frac{a r(\Delta A B C)}{a r(\Delta A D E)}=\frac{B C^{2}}{D E^{2}}$

Subtracting 1 from both sides, we get:

$\frac{\operatorname{ar}(\Delta \mathrm{ABC})}{\operatorname{ar}(\Delta \mathrm{ADE})}-1=\frac{5^{2}}{3^{2}}-1$

$\Rightarrow \frac{\operatorname{ar}(\Delta \mathrm{ABC})-\operatorname{ar}(\Delta \mathrm{ADE})}{\operatorname{ar}(\Delta \mathrm{ADE})}=\frac{25-9}{9}$

$\Rightarrow \frac{\operatorname{ar}(\mathrm{BCED})}{\operatorname{ar}(\Delta \mathrm{ADE})}=\frac{16}{9}$

or, $\frac{\operatorname{ar}(\Delta \mathrm{ADE})}{\operatorname{ar}(\mathrm{BCED})}=\frac{9}{16}$