In the given figure, if PR is tangent to the circle at P and Q is the centre of the circle, then ∠POQ =
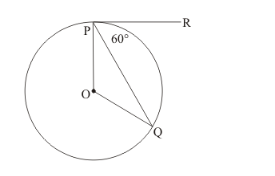
(a) 110°
(b) 100°
(c) 120°
(d) 90°
We know that the radius is always perpendicular to the tangent at the point of contact.
Therefore, we have,
$\angle O P R=90^{\circ}$
It is given that,
$\angle Q P R=60^{\circ}$
That is,
$\angle O P R-\angle O P Q=60^{\circ}$
$90^{\circ}-\angle O P Q=60^{\circ}$
$\angle O P Q=30^{\circ}$
Now, consider $\triangle O P Q$. We have,
OP = OQ (Radii of the same circle)
Since angles opposite to equal side will be equal in a triangle, we have,
![]()
We know that sum of all angles of a triangle will be equal to ![]() .
.
Therefore,
$\angle O P Q+\angle O Q P+\angle P O Q=180^{\circ}$
$30^{\circ}+30^{\circ}+\angle P O Q=180^{\circ}$
$\angle P O Q=120^{\circ}$
The correct answer is option (c).
