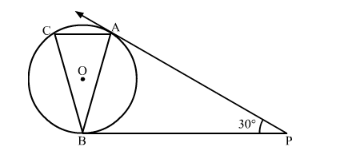
In the given figure, if tangents PA and PB are drawn to a circle such that

We know that tangents from an external point will be equal in length. Therefore,

PA = PB

Now consider . We have,

PA = PB

We know that angles opposite to equal sides will be equal. Therefore,

Also, sum of all angles of a triangle will be equal to .

$\therefore \angle A B P+\angle B A P+\angle P=180^{\circ}$

$2 \angle A B P=180^{\circ}-30^{\circ}$

$2 \angle A B P=150^{\circ}$

$\angle A B P=75^{\circ}$

Now, as $\mathrm{AC} \| \mathrm{PB} ; \angle A B P=\angle C A B=75^{\circ}$ [Alternate interior angles]

Also, $\angle A B P=\angle A C B=75^{\circ}$ [Alternate segment theorem]

In $\triangle \mathrm{ABC}, \angle C A B+\angle A C B+\angle A B C=180^{\circ}$

$75^{\circ}+75^{\circ}+\angle A B C=180^{\circ}$

$\angle A B C=180^{\circ}-150^{\circ}=30^{\circ}$