In the given figure, if TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP = 60°, then ∠OPQ =
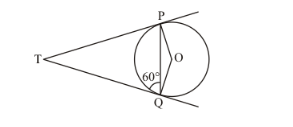
(a) 25°
(b) 30°
(c) 40°
(d) 60°
Consider ![]() .
.
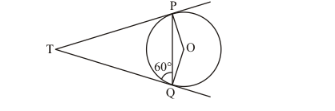
We have,
TP = TQ(Tangents from an external point will be equal)
We know that angles opposite to equal sides will be equal. Therefore,
$\angle T Q P=\angle T P Q$
It is given that,
$\angle T Q P=60^{\circ}$
Therefore,
$\angle T P Q=60^{\circ}$
We know that the radius will always be perpendicular to the tangent at the point of contact. Therefore,
$O P \perp P T$
Hence,
$\angle T P O=90^{\circ}$
That is,
$\angle T P Q+\angle Q P O=90^{\circ}$
We have found that,
$\angle T P Q=60^{\circ}$
Therefore,
$60^{\circ}+\angle Q P O=90^{\circ}$
$\angle Q P O=30^{\circ}$
Therefore, the correct answer is option (b).
