In the given figure, L and M are the mid- points of AB and BC respectively.
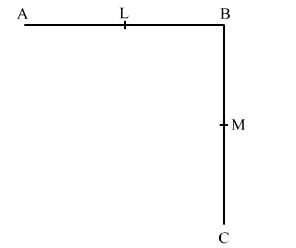
(i) If $A B=B C$, prove that $A L=M C$.
(ii) If $B L=B M$, prove that $A B=B C$.
Hint
(i) $A B=B C \Rightarrow \frac{1}{2} A B=\frac{1}{2} B C \Rightarrow A L=M C$.
(ii) $B L=B M \Rightarrow 2 B L=2 B M \Rightarrow A B=B C$.
(i) It is given that L is the mid-point of AB. ...........(1)
$\therefore \mathrm{AL}=\mathrm{BL}=\frac{1}{2} \mathrm{AB}$
Also, $M$ is the mid-point of $B C$.
$\therefore B M=M C=\frac{1}{2} B C$ ..........(2)
AB = BC (Given)
$\Rightarrow \frac{1}{2} \mathrm{AB}=\frac{1}{2} \mathrm{BC}$ (Things which are halves of the same thing are equal to one another)
⇒ AL = MC [From (1) and (2)]
(ii) It is given that L is the mid-point of AB.
$\therefore \mathrm{AL}=\mathrm{BL}=\frac{1}{2} \mathrm{AB}$
⇒ 2AL = 2BL = AB .....(3)
Also, M is the mid-point of BC.
$\therefore \mathrm{BM}=\mathrm{MC}=\frac{1}{2} \mathrm{BC}$
⇒ 2BM = 2MC = BC .....(4)
BL = BM (Given)
⇒ 2BL = 2BM (Things which are double of the same thing are equal to one another)
⇒ AB = BC [From (3) and (4)]
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.