In the given figure, lines AB and CD intersect at a point O. The sides CA and OB have been produced to E and F respectively such that ∠OAE = x° and ∠DBF = y°.
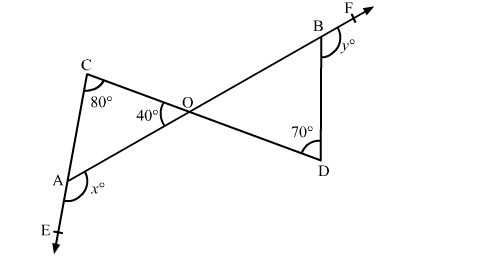
If ∠OCA = 80°, ∠COA = 40° and ∠BDO = 70° then x° + y° = ?
(a) 190°
(b) 230°
(c) 210°
(d) 270°
In the given figure, ∠BOD = ∠COA (Vertically opposite angles)
∴ ∠BOD = 40° .....(1)
In ∆ACO,
∠OAE = ∠OCA + ∠COA (Exterior angle of a triangle is equal to the sum of two opposite interior angles)
⇒ x° = 80° + 40° = 120° .....(2)
In ∆BDO,
∠DBF = ∠BDO + ∠BOD (Exterior angle of a triangle is equal to the sum of two opposite interior angles)
⇒ y° = 70° + 40° = 110° [Using (1)] .....(3)
Adding (2) and (3), we get
x° + y° = 120° + 110° = 230°
Hence, the correct answer is option (b).
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.