Question:
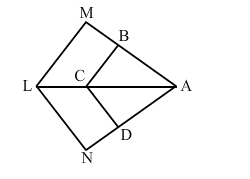
In the given figure, LM CB and LN CD.
Prove that $\frac{A M}{A B}=\frac{A N}{A D}$.
Solution:
$L M \| C B$ and $L N \| C D$
Therefore, applying Thales' theorem, we have:
$\frac{A B}{A M}=\frac{A C}{A L}$ and $\frac{A D}{A N}=\frac{A C}{A L}$
$\Rightarrow \frac{A B}{A M}=\frac{A D}{A N}$
$\therefore \frac{A M}{A B}=\frac{A N}{A D}$
This completes the proof.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.