In the given figure, m and n are two plane mirrors perpendicular to each other.

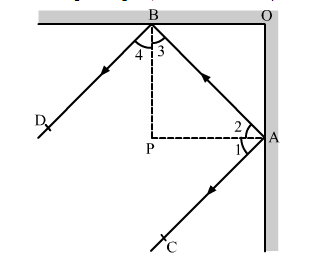
AP is normal to the plane mirror OA and BP is normal to the plane mirror OB.

It is given that the two plane mirrors are perpendicular to each other.

Therefore, BP || OA and AP || OB.

So, BP ⊥ AP       (OA ⊥ OB)

⇒ ∠APB = 90°    .....(1)

In ∆APB,

​∠2 + ∠3 + ∠APB = 180°      (Angle sum property)

∴ ∠2 + ∠3 + 90° = 180°       [Using (1)]

⇒ ∠2 + ∠3 = 180° − 90° = 90°

⇒ 2∠2 + 2∠3 = 2 × 90° = 180°        .....(2)

By law of reflection, we have

∠1 = ∠2  and ∠3 = ∠4                     .....(3)       (Angle of incidence = Angle of reflection)   

From (2) and (3), we have

∠1 + ∠2 + ∠3 + ∠4 = 180°

⇒ ∠BAC + ∠ABD = 180°            (∠1 + ∠2 = ∠BAC and ∠3 + ∠4 = ∠ABD)

Thus, the lines CA and BD are intersected by a transversal AB such that the interior angles on the same side of the transversal are supplementary.

∴ CA || BD