Question:
In the given figure, O is the centre of a circle, ∠AOB 40° and ∠BDC = 100°, find ∠OBC.
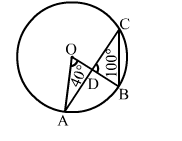
Solution:
We know that the angle subtended by an arc of a circle at the centre is double the angle subtended by the arc at any point on the circumference.
∠AOB = 2∠ACB
= 2∠DCB [∵∠ACB = ∠DCB]
$\therefore \angle D C B=\frac{1}{2} \angle A O B$
$\Rightarrow \angle D C B=\left(\frac{1}{2} \times 40^{\circ}\right)=20^{\circ}$
Considering ΔDBC, we have:
∠BDC + ∠DCB + ∠DBC = 180°
⇒ 100° + 20° + ∠DBC = 180°
⇒ ∠DBC = (180° – 120°) = 60°
⇒ ∠OBC = ∠DBC = 60°
Hence, ∠OBC = 60°
