Question:
In the given figure, O is the centre of a circle and ∠AOC = 120°. Then, ∠BDC = ?
(a) 60°
(b) 45°
(c) 30°
(d) 15°
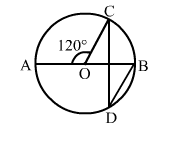
Solution:
(c) 30°
∠COB = 180° - 120° = 60° (Linear pair)
Now, arc BC subtends ∠COB at the centre and ∠BDC at the point D of the remaining part of the circle.
∴ ∠COB = 2∠BDC
$\Rightarrow \angle \mathrm{BDC}=\frac{1}{2} \angle \mathrm{COB}=\left(\frac{1}{2} \times 60^{\circ}\right)=30^{\circ}$
