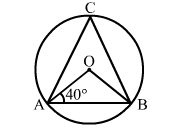
Question:
In the given figure, O is the centre of a circle. If ∠OAB = 40° and C is a point on the circle, then ∠ACB = ?
(a) 40°
(b) 50°
(c) 80°
(d) 100°
Solution:
(b) 50°
OA = OB
⇒ ∠OBA = ∠OAB = 40°
Now, ∠AOB = 180° - (40° + 40°) = 100°
$\therefore \angle \mathrm{ACB}=\frac{1}{2} \angle \mathrm{AOB}=\left(\frac{1}{2} \times 100\right)^{\circ}=50^{\circ}$
