Question:
In the given figure, O is the centre of a circle in which ∠OAB = 20° and ∠OCB = 55°. Find ]\
(i) ∠BOC,
(ii) ∠AOC
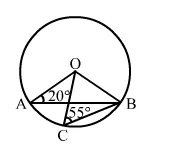
Solution:
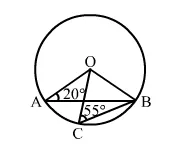
(i)
OB = OC (Radii of a circle)
⇒ ∠OBC = ∠OCB = 55°
Considering ΔBOC, we have:
∠BOC + ∠OCB + ∠OBC = 180° (Angle sum property of a triangle)
⇒∠BOC + 55° + 55° = 180°
⇒∠BOC = (180° - 110°) = 70°
(ii)
OA = OB (Radii of a circle)
⇒ ∠OBA = ∠OAB = 20°
Considering ΔAOB, we have:
∠AOB + ∠OAB + ∠OBA = 180° (Angle sum property of a triangle)
⇒∠AOB + 20° + 20° = 180°
⇒∠AOB = (180° - 40°) = 140°
∴ ∠AOC = ∠AOB - ∠BOC
= (140° - 70°)
= 70°
Hence, ∠AOC = 70°
