Question:
In the given figure, O is the centre of a circle in which ∠OBA = 20° and ∠OCA = 30°. Then, ∠BOC = ?
(a) 50°
(b) 90°
(c) 100°
(d) 130°
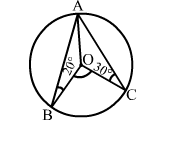
Solution:
(c) 100°
In Δ OAB, we have:
OA = OB (Radii of a circle)
⇒ ∠OAB = ∠OBA = 20°
In ΔOAC, we have:
OA = OC (Radii of a circle)
⇒ ∠OAC = ∠OCA = 30°
Now, ∠BAC = (20° + 30°) = 50°
∴ ∠BOC = (2 × ∠BAC) = (2 × 50°) = 100°
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
