In the given figure, O is the centre of the circle,

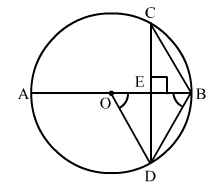
In the given figure, BD = OD and CD ⊥ AB.

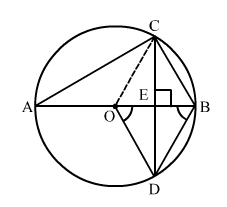
Join AC and OC.

In ∆ODE and ∆DBE,
∠DOE  = ∠DBE      (given)
∠DEO  = ∠DEB = 90∘
OD = DB     (given)
∴ By AAS conguence rule, ∆ODE ≌ ∆BDE,

Thus, OE = EB        ...(1)

Now, in ∆COE and ∆CBE,
CE  = CE      (common)
∠CEO  = ∠CEB = 90∘
OE = EB     (from (1))
∴ By SAS conguence rule, ∆COE ≌ ∆CBE,

Thus, CO = CB        ...(2)

Also, CO = OB = OA (radius of the circle)         ...(3)

From (2) and (3),
CO = CB = OB
∴ ∆COB is equilateral triangle.
∴ ∠COB  = 60∘         ...(4)

We know that the angle subtended by an arc of a circle at the centre is double the angle subtended by it on the remaining part  of the circle.

Here, arc CB subtends ∠COB at the centre and ∠CAB at A on the circle.

∴ ∠COB = 2∠CAB

$\Rightarrow \angle C A B=\frac{60^{\circ}}{2}=30^{\circ}$         (from (4))

Hence, ∠CAB = 30∘.