In the given figure, O is the centre of two concentric circles of radii 4 cm and 6 cm respectively.

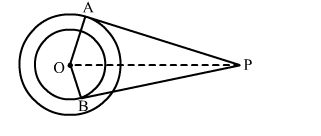
Given, $O$ is the centre of two concentric circles of radii $O A=6 \mathrm{~cm}$ and $O B=4 \mathrm{~cm}$.

$P A$ and $P B$ are the two tangents to the outer and inner circles respectively and $P A=10 \mathrm{~cm}$.

Now, tangent drawn from an external point is perpendicular to the radius at the point of contact.

$\therefore \angle O A P=\angle O B P=90^{\circ}$

$\therefore$ From right-angled $\triangle O A P, O P^{2}=O A^{2}+P A^{2}$

$=>O P=\sqrt{O A^{2}+P A^{2}}$

$=>O P=\sqrt{6^{2}+10^{2}}$

$=>O P=\sqrt{136} \mathrm{~cm}$

$\therefore$ From right-angled $\triangle O A P, O P^{2}=O B^{2}+P B^{2}$

$=>P B=\sqrt{O P^{2}-O B^{2}}$

$=>P B=\sqrt{136-16}$

$=>P B=\sqrt{120} \mathrm{~cm}$

$=>P B=10.9 \mathrm{~cm} .$

$\therefore$ The length of $P B$ is $10.9 \mathrm{~cm}$.