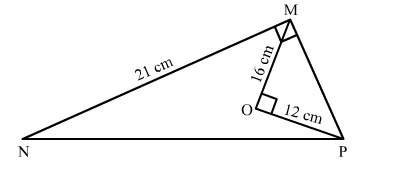
In the given figure, O is the point inside a △MNP such that ∠MOP = 900 ,

Now, In right triangle MOP
By using Pythagoras theorem, we have

$\mathrm{MP}^{2}=\mathrm{PO}^{2}+\mathrm{OM}^{2}$

$=12^{2}+16^{2}$

$=144+256$

$=400$

$\therefore \mathrm{MP}^{2}=400$

$\Rightarrow \mathrm{MP}=20 \mathrm{~cm}$

Now, In right triangle MPN
By using Pythagoras theorem, we have

$\mathrm{PN}^{2}=\mathrm{NM}^{2}+\mathrm{MP}^{2}$

$=21^{2}+20^{2}$

$=441+400$

$=841$

$\therefore \mathrm{MP}^{2}=841$

$\Rightarrow \mathrm{MP}=29 \mathrm{~cm}$

Hence, the correct answer is option (b).