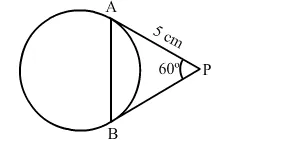
In the given figure, PA and PB are tangents to the given circle, such that PA = 5 cm and ∠APB = 60°.

(b) 5 cm
The lengths of tangents drawn from a point to a circle are equal.

So, $P A=P B$ and therefore, $\angle P A B=\angle P B A=x$ (say).

Then, in $\Delta P A B$ :

$\angle P A B+\angle P B A+\angle A P B=180^{\circ}$

$\Rightarrow x+x+60^{\circ}=180^{\circ}$

$\Rightarrow 2 x=180^{\circ}-60^{\circ}$

$\Rightarrow 2 x=120^{\circ}$

$\Rightarrow x=60^{\circ}$

$\therefore$ Each angle of $\triangle P A B$ is $60^{\circ}$ and therefore, it is an equilateral triangle.

$\therefore A B=P A=P B=5 \mathrm{~cm}$

$\therefore$ The length of the chord $A B$ is $5 \mathrm{~cm}$.