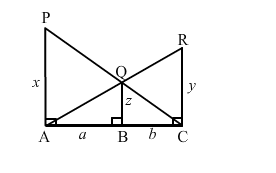
In the given figure, PA, QB and RC are perpendicular to AC. If AP = x, QB = z, RC = y,

In $\triangle P A C$ and $\triangle Q B C$, we have :

$\angle A=\angle B \quad\left(\right.$ Both angles are $\left.90^{\circ}\right)$

$\angle P=\angle Q \quad$ (Correspond ing angles)

and

$\angle C=\angle C \quad$ (Common angles)

Therefore, $\triangle P A C \sim \triangle Q B C$

$\frac{A P}{B Q}=\frac{A C}{B C}$

$\Rightarrow \frac{x}{z}=\frac{a+b}{b}$

$\Rightarrow a+b=\frac{b x}{z} \quad \ldots(1)$

In $\triangle R C A$ and $\triangle Q B A$, we have :

$\angle C=\angle B \quad\left(\right.$ Both angles are $\left.90^{\circ}\right)$

$\angle R=\angle Q \quad$ (Correspond ing angles)

and

$\angle A=\angle A \quad$ (Common angles)

Therefore, $\triangle R C A \sim \triangle Q B A$

$\frac{R C}{B Q}=\frac{A C}{A B}$

$\Rightarrow \frac{y}{z}=\frac{a+b}{a}$

$\Rightarrow a+b=\frac{a y}{z} \quad \ldots(2)$

From equation (1) and (2), we have:

$\frac{b x}{z}=\frac{a y}{z}$

$\Rightarrow b x=a y$

$\Rightarrow \frac{a}{b}=\frac{x}{y} \quad \ldots(3)$

Also,

$\frac{x}{z}=\frac{a+b}{b}$

$\Rightarrow \frac{x}{z}=\frac{a}{b}+1$

Using the value of $\frac{a}{b}$ from equation $(3)$, we have:

$\Rightarrow \frac{x}{z}=\frac{x}{y}+1$

Dividing both sides by $x$, we get:

$\frac{1}{z}=\frac{1}{y}+\frac{1}{x}$

$\therefore \frac{1}{x}+\frac{1}{y}=\frac{1}{z}$

This completes the proof.