In the given figure, PO ⊥ QO. The tangents to the circle at P and Q intersect at a point T

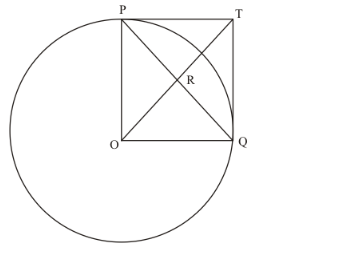
In the given figure,

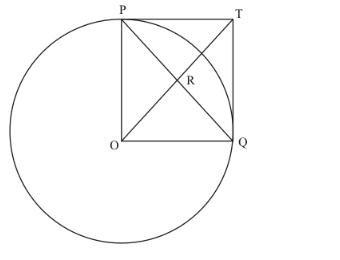
PO = OQ (Since they are the radii of the same circle)

PT = TQ (Length of the tangents from an external point to the circle will be equal) Now considering the angles of the quadrilateral PTQO, we have,

 (Given in the problem)

 (The radius of the circle will be perpendicular to the tangent at the point of contact)

 (The radius of the circle will be perpendicular to the tangent at the point of contact)

We know that the sum of all angles of a quadrilateral will be equal to . Therefore,

$\angle P O Q+\angle T Q O+\angle O P T+\angle P T Q=360^{\circ}$

$90^{\circ}+90^{\circ}+90^{\circ}+\angle P T Q=360^{\circ}$

$\angle P T Q=90^{\circ}$

Thus we have found that all angles of the quadrilateral are equal to 90°.

Since all angles of the quadrilateral PTQO are equal to 90° and the adjacent sides are equal, this quadrilateral is a square.

We know that in a square, the diagonals will bisect each other at right angles.

Therefore, PQ and OT bisect each other at right angles.

Thus we have proved.