In the given figure, points A, B, C and D are the centres of four circles that each have

Solution:

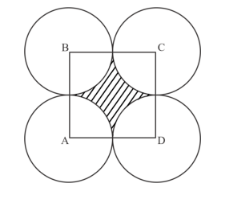
Given: A, B, C, and D are the centers of four circles that each have a radius of length one unit. If a point is selected at random from the interior of square ABCD

To find: Probability that the point will be chosen from the shaded region,

In the figure we can see 4 circles of radius 1 unit.

Area of quarter circle with centre A:

$=\frac{1}{4}\left(\pi r^{2}\right)$

$=\frac{1}{4}\left(\pi \times 1^{2}\right)$

$=\frac{\pi}{4}$

Since all the circles are of the same radius, hence the area of quarter with centre B, C, D will be same as the area of circle of quarter of circle with centre A.

Hence total area covered by 4 quarter circle will be

$=4\left(\frac{\pi}{4}\right)$

$=\pi$ unit $^{2}$

Side of the square will be 2 units

Area of square ABCD = 4 unit2

Area of the shaded portion 

We know that PROBABILITY

$=\frac{\text { Number of favourable event }}{\text { Total number of event }}$

$=\frac{4-\pi}{4}$

 

$=1-\frac{\pi}{4}$

Hence probability of the shaded region is $1-\frac{\pi}{4}$