In the given figure, PQ is tangent at a point R of the circle

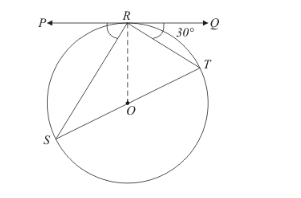
We have been given that $\angle T R Q=30^{\circ}$.

From the property of tangents we know that a tangent will always be perpendicular to the radius at the point of contact. Therefore,

Looking at the given figure we can rewrite the above equation as follows,

We know that. Therefore,

$30^{\circ}+\angle T R O=90^{\circ}$

$\angle T R O=60^{\circ}$

Now consider. The two sides of this triangle OR and OT are nothing but the radii of the same circle. Therefore,

OR = OT

And hence is an isosceles triangle. We know that the angles opposite to the equal sides of the isosceles triangle will be equal. Therefore,

We have found out that. Therefore,

= 

Now consider. We know that sum of all angles of a triangle will always be equal to . Therefore,

$\angle T R O+\angle O T R+\angle T O R=180^{\circ}$

$60^{\circ}+60^{\circ}+\angle T O R=180^{\circ}$

$\angle T O R=60^{\circ}$

Now let us consider the straight line SOT. We know that the angle of a straight line is . Therefore,

$\angle S O T=180^{\circ}$

From the figure we can see that,

$\angle S O T=\angle S O R+\angle T O R$

That is,

$\angle S O R+\angle T O R=180^{\circ}$

We have found out that $\angle T O R=60^{\circ}$. Therefore,

$\angle S O R+60^{\circ}=180^{\circ}$

$\angle S O R=120^{\circ}$

Let us take up now. The sides SO and OR of this triangle are nothing but the radii of the same circle and hence they are equal. Therefore,is an isosceles triangle. In an isosceles triangle, the angles opposite to the two equal sides of the triangle will be equal. Therefore we have,

$\angle O S R=\angle O R S$

Also the sum of all angles of a triangle will be equal to. Therefore,

$\angle S O R+\angle O R S+\angle O S R=180^{\circ}$

$\angle S O R+2 \angle O R S=180^{\circ}$

In the previous step we have found out that. Therefore,

$120^{\circ}+2 \angle O R S=180^{\circ}$

$2 \angle O R S=60^{\circ}$

$\angle O R S=30^{\circ}$

Let us now take up . We know from the property of tangents that the angle between the radius of the circle and the tangent at the point of contact will be equal to . Therefore,

$\angle O R P=90^{\circ}$

By looking at the figure we can rewrite the above equation as follows,

$\angle P R S+\angle O R S=90^{\circ}$

In the previous section we have found that. Therefore,

$\angle P R S+30^{\circ}=90^{\circ}$

$\angle P R S=60^{\circ}$

Thus we have found out that .